Lesson 3 Theory of (complex) systems
This lesson is dedicated to systems theory, the theory behind simulation modelling. Systems theory is an interdisciplinary branch of science that conceptualises systems as a group of interacting elements that together form a complex whole that is more than the sum of its parts. The central idea of “wholeness” of a system stands in stark contrast to conventional science that is based upon Descartes’s reductionism, where the aim is to analyse systems by reducing something to its component parts (Cham and Johnson 2007). Simulation modelling is the method to reproduce a system of interest in a “virtual lab” in order to predict, better understand or design future scenarios of systems.
3.1 More than the sum..
A central aspect of the nature of a system can be sketched in a popular saying:
A system is greater than the sum of its parts
Traditional scientific approaches are focused on getting a better understanding of the world by ‘dissecting’ our complex environment into its parts and then establish cause – effect relationships. Chemists and physicists dissected material to molecules, molecules to atoms, atoms to positrons and electrons and so forth. Accordingly, biologists tried to make sense of the environment by dissecting it to single species, and further to single animals, studying their individual behaviour and their physiology. This reductionist view of the world was juxtaposed by a holistic world view by system thinkers, who postulated that a system has a behaviour of its own and that such system behaviour can only be explained by studying the system as a whole. A population of animals behaves differently as we would expect from the behaviour of isolated animals. Just as a stock market follows rules of its own.

Figure 3.1: The whole is more than the sum of its parts. Only a holistic view allows us to understand a system.
Let’s consider the hydrological cycle in an ecosystem. First, we are looking for internally homogenous parts of the ecosystem that are relevant in order to model the flow of water through the system. Each of these system elements holds a certain amount of water: clouds, snow, rivers, soil. The interrelation between the stocks is water that flows from one stock into another with a defined direction, e.g.: precipitation, snowmelt runoff, infiltration to groundwater, evaporation. We have now successfully designed a conceptual model of a system that has the function to perpetuate the flow of water through an ecosystem.
Another example is the human digestive system: It consists of different organs (stomach, intestine, liver, etc.) which are connected with the purpose of converting food into energy and waste.
These are two examples of ‘open systems’ in which we gain and loose material or energy in flows to the outside environment.
3.2 General Systems Theory
The ‘father’ of Systems Theory was the biologist Ludwig Bertalanffy (1901-1972). In his General Systems Theory, Bertalanffy proposed his view of a science of ‘wholeness’: He postulated to consider ecosystems as ‘open systems’ that consist of a set of elements and their relations. According to Bertalanffy, in the ‘organised complexity’ of an open system, there is no simple linear coupling, but complex interrelations that govern non-linear system behaviour. Bertalanffy proposed systems thinking as a new and integrative way to discover how system elements interact with their environment.

Figure 3.2: Ludwig Bertalanffy (1901-1972): the father of General Systems Theory.
In living systems, there cannot be an equilibrium as there is always a flow of energy and material in and out of the system. For example, with every breath we take, oxygen enters the body and carbon dioxide exits. Nevertheless, the human body manages to keep its system at constant levels. Bertalanffy addressed this quasi-equilibrium of open systems as ‘steady state’. This concept of a steady state that is inherent to an open system is an outstanding and vital property of living systems. Table 3.1 juxtaposes closed and open systems.
| Closed systems | Open systems |
|---|---|
| persistent | constantly fluctuating |
| equilibrium | steady state |
| equilibria are based on reversible reactions | steady states are irreversible |
| final state is deterministic | self-organising and equifinal states |
Whereas traditional experiments are conducted in closed systems, the real world is an open system that behaves fundamentally different from the closed systems that we encounter in strictly controlled environments of classical experiments.
3.2.1 Open systems
General Systems Theory provides the theoretic body to think about, formalise and study open systems and thus lays the foundation for the analysis and modelling of open systems.
Systems that are considered open systems…
- are characterised by a constant flow of material and energy into and out of the system: These systems are ‘open’ to the surrounding environment.
- can never reach an equilibrium in the strict sense of the word, which is defined by an absolute stagnation of the flows of energy and matter. However, there is a dynamic equilibrium, which is referred to as ‘steady state’.
- are self-organising and generate highly structured organisms. This is in contrast to closed systems that develop towards a state of maximum disorder (= entropy) according to the 2nd Law of Thermodynamics.
- develop towards an irreversible steady state that is independent from initial conditions; for example, the frequency of a human heart beat will always be the same on average, independent from the heart beat at the time of birth. This behaviour is called ‘equifinality’. In contrast to that, closed systems reach a final state that is deterministically dependent on its initial conditions.
- are kept in balance (homeostasis) by self-regulating feedback loops. Only open systems allow life to ‘work’.
The General Systems Theory was developed in the background of natural sciences, but subsequently it inspired scholars across many, fundamentally different domains and disciplines, including biology, psychology, sociology, engineering and economics. Some scholars advanced the theoretical and epistemological foundation, some focused on the applied side. Shaped by their backgrounds, system thinkers developed different schools of systems theory. In Figure 3.3 Hieronymi (2013) provides an overview of different schools of thought in systems research and their most influential scholars.
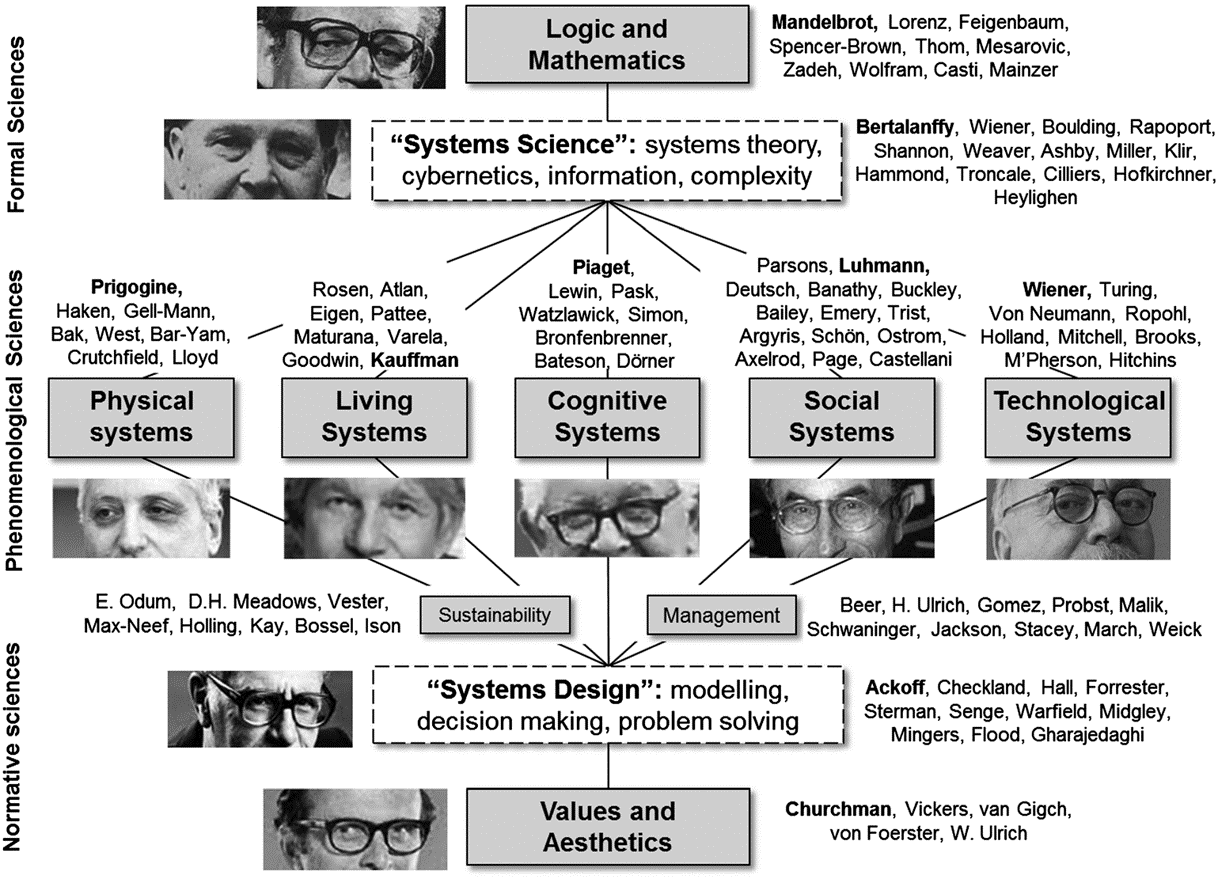
Figure 3.3: In this rubric, leading system thinkers are positioned according to their domain and approach. Source: Hieronymi (2013)
3.3 System components
To be able to represent a system in a model, we need to have a conceptual understanding of the system; that is: we need to have a conceptual model. To come up with such conceptual model, it is helpful to think about the components of a system:
“A system is an interconnected set of elements that is coherently organized in a way that achieves something” (Meadows and Wright 2008)
So, in short a system (and thus also a model of a system) consists of three components: 1) elements, 2) interconnections, and 3) a purpose or function. All three components are essential. If there was just an agglomeration of elements without connection and without purpose – for example a pile of sand – it would not be a system. When a living creature dies, it loses its ‘system-ness’. A football team can be viewed as a system: its elements are players, coach, field, and ball. Its interconnections are the rules of the game, the coach’s strategy, the players’ communications, and the laws of physics that govern the motions of the ball and the players. The purpose of the team is to win the game.
Elements are often the easiest part to conceptualise. A transportation system consists of streets, trucks, goods to be delivered, truck drivers, etc. An educational system is composed of a school or university campus, students, professors, etc. The football team would still function more or less the same way, even if we exchange each player. A university stays the same university, although generations of students pass through.
Interconnections hold everything together, they define the structure and the functioning of a system. What would happen, if we change the rules that a football must not be touched with feet, but only with hands? If students grade professors?
Changing its purpose affects a system most fundamentally. How would a football team function, that has the purpose to lose, instead of winning? How would a university look like that aims at persuading students of the ‘single truth’.
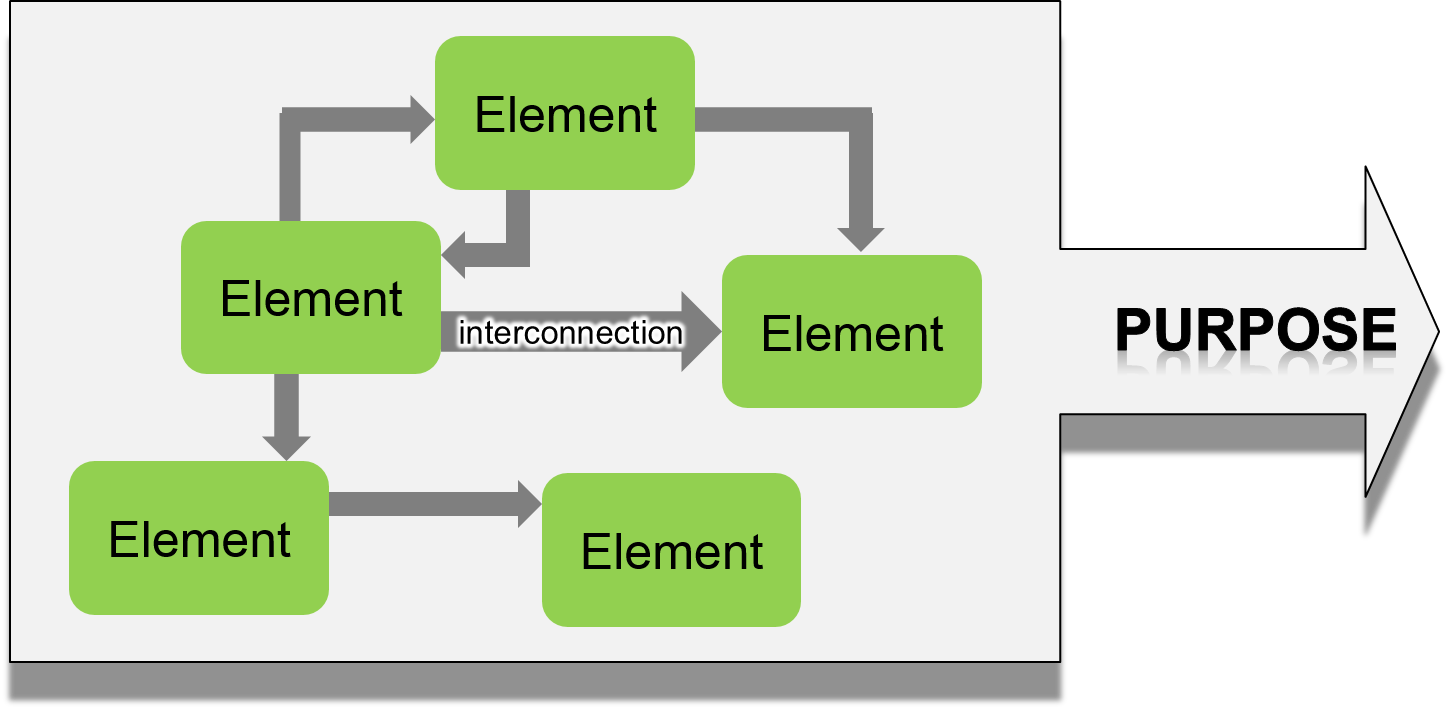
Figure 3.5: The three components of a system: elements, interconnections, purpose.
3.4 Complexity Theory
What would happen, if a bunch of the brightest scientists of the time from domains as different as physics, economy and computer science came together for a workshop to define the essence of what they all feel to be an emerging new approach in science? What if there were enough funds to found a research institute without any departmental boundaries to offer these researchers a place to collaborate and develop their ideas further? The result would probably be a promising new way of thinking – a new theory that brings about a paradigmatic change.
This is in short the story of the Santa Fe Institute in New Mexico and how Complexity Theory was developed. Shaping Complexity Theory has been a collaborative endeavour. However, if I was to name one ‘father’ of complexity this would most likely be John Holland, who published the Theory of Complex Adaptive Systems (Holland 1992).

Figure 3.6: John Holland (1919 - 2015), one of the leading scholars in the development of the complexity theory.
Here is an excerpt from Santa Fe’s website (http://www.santafe.edu):
In 1975, Holland published the groundbreaking book Adaptation in Natural and Artificial Systems, which has been cited more than 50,000 times. Intended to be the foundation for a general theory of adaptation, this book introduced genetic algorithms as a mathematical idealization that Holland used to develop his theory of schemata in adaptive systems. Later, genetic algorithms became widely used as an optimization and search method in computer science.
Complexity Theory is a systems theory just like the General System Theory. It builds on the assumption that the whole is more than the sum of its parts. Complexity Theory also conceptualises the structure of systems to be made of elements that are connected together. It proposes that systems are non linear, so that small catalysts can cause large changes and that systems are self-organising. However, in difference to the General Systems Theory it works bottom-up, with interacting individuals as its basic elements.
In the geospatial domain, complex systems are of particular interest, because local spatial configuration provides the structure for interactions between individual entities in the system. Whereas traditional simulation modelling approaches that rooted in systems theory chiefly were concerned with non-spatial temporal progression, complexity theory is equally concerned with both, time and space (O’Sullivan 2004).
In the following, the main characteristics of complex systems are presented and exemplified with interactive toy models. The software to show these models is NetLogo Web, the browser-based version of NetLogo, which is a popular programming environment to develop agent-based models. This open-source software is authored by Uri Wilensky and it is widely used by the modelling community to develop agent-based models and cellular automata. You can explore and even modify NetLogo models online through NetLogo Web.
3.4.1 Individuals are unique
Central to the philosophy of complexity is that no individual is like the other. Each member of a population differs from its mates or peers in sex, age, size or colour. More profoundly it also differs in memory, experience and behaviour. Between some individuals there are stronger social bounds than between others. Not least from a geographic perspective individuals differ by location. Even if all individuals were the same, these individuals would differ by their spatial context: one would be closer to a food source, or more in the centre of the protecting crowd, or it would occupy a superior nesting site.
The richer the behavioural variety of a species, the stronger will individuals differ and the less suited are general system models that are based on differential equations of “stocks” and thus assume that the individuals in a system are all equal. A striking example of this concept was published in the influential, first review paper on Agent-based models in the Ecological domain by Huston, DeAngelis, and Post (1988): Figure 3.7 shows that a general system model with equal individuals completely differs from a complex system that consists of unique, spatial individuals.
![Small individual differences in individuals (here: tree size) can cause distinctly different results on the system level (here: forest stand structure). Modified after Huston et al. [-@huston1988].](images/emergence-from-heterogeneity.png)
Figure 3.7: Small individual differences in individuals (here: tree size) can cause distinctly different results on the system level (here: forest stand structure). Modified after Huston et al. (1988).
Figure 3.8 is an interactive model that reproduces the results published by Huston, DeAngelis, and Post (1988).
To initialise the model, press the setup button and to run the simulation, click go. You can see the tree biomass histogram bar move from left to right, as the forest grows. Now, check the “spatial” box, setup the model again and run it. Can you explain, why the model results in a bimodal distribution in the histogram of tree biomass? Or in other words: why are there just few big trees and so many small trees?
Figure 3.8: Forest of equal vs. unique trees, NetLogo Web
See solution!
Bigger trees are more competitive than smaller trees, as they reach more resources like light, water or nutrients. Solitary, big trees thus grow faster and inhibit the growth of smaller trees in their neighbourhood.
3.4.2 Individuals adapt
An individual’s ability to adapt is the second fundamental difference between conventional and complex systems after heterogeneity of individuals. Such capability can be encoded in behavioural rules, but it is not mathematically tractable.
Adaptation can refer to immediate response to a situation, or it can initiate learning processes that may manifest in later actions, or it can trigger long-term evolution through genetic exchange, mutation and selection.
Figure 3.9 shows the model of a famous example for genetic evolution in response to environmental change. Due to severe air pollution following the industrial revolution, white birch trees near Manchester, England, turned black. For a specific white-coloured moth species this turned out to be a real problem, because suddenly birds could easily spot them, and the number of Biston popularia (peppered moth) declined drastically. However, after some generations, mutations of darker morphs appeared and the population survived.
Again, click on setup and then on go to run the peppered moths model. While the simulation runs, pollute (click the button several times) the environment. Can you see, how the moth population adapts to the darker colour, because well-adapted individuals have a higher survival probability?
Figure 3.9: Peppered Moths model, NetLogo Web
3.4.3 Emergence
The unique characteristic of complex systems is emergence: the non-intuitive formation of system-level patterns from the interaction of individuals with their neighbours and the local environment. It is the contrary to top-down imposed behaviour. Emergence is rooted in the structure of a complex system, which is defined by the connections between individual entities (remember the social theory of Luhman: communication links are more important for a society than individual persons). Thus, the interactions between entities lead to the emergence of complex system patterns such as bee hives, schools of fish, commuting patterns and social communities.
If there is a specific set of links and interactions types between individuals (such as the social behaviour of bees), similar systems (bee colonies) will emerge. Also for the much richer human behaviour, similar system patterns emerge in a largely self-organised way: urban street networks, communication clusters or food supply chains.
Grimm and Railsback (2013) identify three criteria of emergent behaviour:
- Emergent properties are not simply the sum of the properties of the individuals
- Emergent properties are of a different type than the properties of the individuals (e.g. the spatial distribution of individuals is a system property of a type that none of the system’s individuals has)
- Emergent properties are often counterintuitive and cannot easily be predicted by looking only at the individuals.
To better understand the concept of emergence, which is central to systems thinking and modelling, take a cup of tea and watch the video below (Figure 3.10). It explains the concept with nice visualisations and a couple of examples.
Figure 3.10: Video 7:30 min. Emergence - how stupid things become smart.
A strikingly simple and yet fascinating example of emergent patterns is the generation of clustered movement (“flocking”) in social animals. Let’s explore it further in the following exercise.
Now, explore emerging patterns yourself by playing around with the flocking model (Figure 3.11). The model is based on the work by Reynolds (1987) and it has been implemented in NetLogo Web.
The flocking model has five parameters. Move the individual sliders and you will immediately see how the birds’ behaviour changes. Can you find a parameter setting, in which the flock does not move forward into any direction, but just builds a stationary flock, like midges sometimes do, when they dance around themselves?
Figure 3.11: Netlogo Flocking Model
See solution!
In a stationary flock, midges fly towards each other, if they feel separated, and they turn away to avoid collisions with other midges. However, they never align their flight direction, because they don’t want to travel anywhere.
That means: set the max-cohere-turn slider and the max-separate-turn slider to the maximum (20 degrees) and reduce the max-align-turn to zero.
3.4.4 Self-similarity
Complex systems emerge from iterative processes. As a result, the emerging patterns often repeat themselves at different levels of scale: when we paddle up a river we will see it bifurcate repeatedly until we reach the spring. Analogously, informal settlements consist of shelters, which are part of a block, which in turn is part of a quarter – an emergent pattern that was not planned by any city government. The same is true for coast lines, trees, ferns or ice crystals. An almost perfect example for a natural self-similar pattern is the Romanesque Broccoli.
The hierarchical structure of self similar systems can be described mathematically as fractals. The idea of fractal dimensions was pioneered by Benoit Mandelbrot. The fractal dimension is a ratio that provides a statistical index of complexity: it compares how the detail in a pattern changes with scale at which it is measured. This mathematical approach to self-similarity helps us in describing such patterns in a quantitative way.
Figure 3.12 shows a snowflake that perfectly repeats the pattern of its boundaries as one zooms in. It is known as the Koch Snowflake. Hover your mouse over the image to see!
Figure 3.12: The Koch snowflake is a perfect self-similar structure: as you hover your mouse over the image it zooms in and repeats its pattern over an endless level of scales.
3.4.5 Stochasticity
In a model of a complex system, every action and interaction depends on the condition, experience and environment of each individual at its certain location and the specific connections between the individuals at that certain point in time. As you can imagine these situations result in pretty unpredictable processes. However, the processes are not completely random, they are stochastic: common behavioural rules and social bounds bring order into the chaos and over time consistent patterns evolve (that is: emerge!).
Simulate the first 200 time steps of the same virus model 3.13 with the same parameters several times. As this model nicely demonstrates, one will never be able to exactly predict the future of a complex system, but a modeller can discover underlying processes and unveil trends that are inherent to that system.
Figure 3.13: The virus model is a stochastic model: although it always exhibits the same patterns, each simulation run is different.
3.4.6 Swarm intelligence
One major implication from Complexity Theory is widely known under the keyword “swarm intelligence”. The idea behind this concept is that from a large enough crowd of ‘stupid’, interacting individuals, an unexpectedly smart collective behaviour arises. An often cited example for swarm intelligence are fire ants that build floating bridges over water, once their nest is flooded. Although individual ants may die, the colony itself survives. A less drastic examples comes from homing pigeon flocks that are more efficient when flying in flocks compared to singleton flights.
A good example for this phenomenon is the Ants model embedded in Figure 3.14 below. Click the setup button and let the model run. You will see ants spawning from the ants nest in the middle and starting to run around randomly. Once they come across food, they pick it up and move back towards their nest. In doing so, they leave behind a chemical trail. This trail enables the other ants to also find this food source and they start to move between the food source and their nest until is depleted. What seems to be random in the beginning starts to become organised without direct communication between the ants.
Figure 3.14: Netlogo Ants Model
In computer engineering the concept of swarm intelligence is utilised to find solutions for mathematically intractable or computationally too expensive calculations. The so-called heuristic algorithms do not provide the best solution, but are very good in quickly finding a good solution. An example is the ‘ant colony optimisation’ algorithm for finding the short paths through a network. Click on Figure 3.15 to see, how the algorithms works.
Figure 3.15: The ant colony optimisation algorithm is a computational heuristic for path finding that builds on the swarm intelligence of ants. Click on the figure to the algorithm at work. Animation from: https://graph-algorithm-showcase.info/
3.5 General and Complex Systems
What is the common denominator of systems that we have discussed in the context of Bertlanffy’s General Systems Theory and the ‘new’ Complex Systems? The shared idea of both, closely related theories is that a system is a holistic entity that emerges and evolves from the interrelation of its components. A system behaves in an often unexpected and complex way and it has a set of properties that cannot be explained - or modelled - with a reductionist approach.
- Non-linearity Minor changes in the initial conditions can lead to surprising shifts in the behaviour of the system. Non-linearity is due to the internal structure of complex systems.
- Feedback Feedback loops regulate (balancing feedback) or deregulate (reinforcing feedback) parts of a system. Examples for balancing feedback are abundant in natural ecosystems. However, in disturbed ecosystems, we sometimes witness positive feedback loops to govern the system and lead to an ecosystem ‘collapse’, e.g. an invasive species that colonises a vacant ecological niche and thus finds largely unlimited resources.
- Self organisation is the ability of system elements to learn, diversify, complexity and evolve so that some sort of ‘global order’ (structure at system level) arises from local interaction. For example: the growth of a living organism from a fertilised egg, or the coordination of a school of fish or flock of birds. The property of self-organisation is frequently found in living systems, however it also can be observed in snowflakes that grow from a single grain of ice or crystals that grow in supersaturated solutions.
- Nested hierarchy In a nested hierarchy the elements at each level self-organise into a greater whole that is more than the sum of its parts. For example: an atom is part of a molecule, which is part of a cell, which is part of an organ, which is part of a body, which is part of a society. The interrelations between elements of one subsystem are much denser and stronger than outside relationships. This way each sub-system can regulate and organise itself, although it is still firmly anchored within the context of its sub- and super-systems.
- Resilience is the ability of a system to recover after disturbance. An example is the regrowth of trees after forest fires or the recovery of an economic system after stock market crash.
- Path dependence Not only the current state, but also the past influences future dynamics.
3.2.2 Social Systems
The German sociologist Niklas Luhmann is widely acknowledged in his field as on of the most influential thinkers of the 20th century. The amount of his scientific output was tremendous with more than 70 books and 400 scholarly articles. As he used to publish in German language, his work is less known in the anglophone world. However, it was intensively received in parts of Europe, Japan and Russia.
Figure 3.4: Niklas Luhmann (1927 - 1998): A social system is constituted by the communication links between individual people.
Luhmann referred to theories and concepts of systems theory and transferred it into the domain of sociology. The core of Luhmann’s social theory builds on communication as the link between social entities. Through communication links a social structure emerges. He argues that communication links constitutes a social System. In contrast, individual people are system entities and as such can be exchanged without changing the societal system as a whole.
Luhmann himself termed his theory of social systems “labyrinth-like” and thus difficult to explain in a concise manner. Anyone, who has an in-depth interest in Luhmann’s theories is therefore referred to his own work or to the abundant secondary literature.