Lesson 4 Models of spatial systems
This lesson provides an overview on different approaches to model systems in a spatially explicit way. We will first look into equation-based approaches, including Spatial System Dynamics and Partial Differential Equation (Finite Element) models. Then briefly introduce into probability-based models like Markov Chains and Bayesian models. Most importantly, finally this lesson focusses on the rule-based approaches of Geosimulation that include Agent-based modelling and Cellular Automata, which are at the core of this module.
4.1 Approaches to spatial models
To set the stage discussing potential approaches to model systems in a spatially explicit way, let me refer back to the three components of a system: entities, connections and the purpose. The way, how these components are conceptualised in the model and represented in the computer leads to complementary modelling approaches.
Spatial entities can be modelled as cells in a grid, patches in a landscape coverage, individual points in a specified area, or nodes in a network. The spatial resolution thereby represents the scale of the local processes of individual entities, e.g. to accommodate dispersal processes or foraging ranges. The spatial extent defines the spatial boundaries of the system.
The connections between entities are defined by local ranges (e.g. buffers, or field of views around points) or neighbourhood definitions (e.g. adjacent polygons of a patch).
Processes can be represented with help of differential equations, probability functions or behaviour rules. These processes include interactions between connected entities, interactions of an entity with the local environment and processes of each entity from one time step to another.
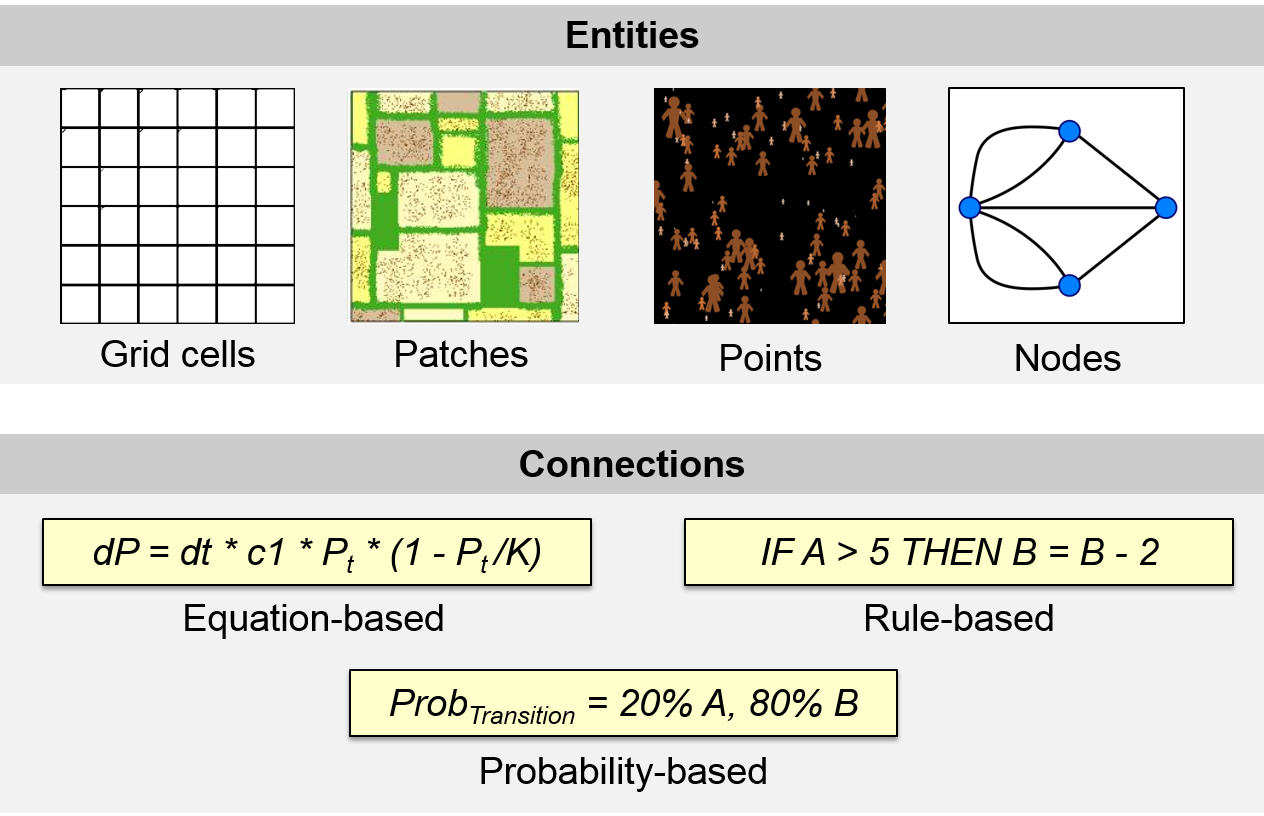
Figure 4.1: A conceptual framework to approach possible representations of spatial systems in a computer model: the building blocks are spatial entities represented as raster cells, polygons, points, or networks and their connections can be implemented as equations, rules or statistical probabilities.
From connecting alternative representations of spatial entities with alternative representations of processes to link these entities we can derive a systematic overview of methodological approaches to spatial simulation (Figure 4.2).
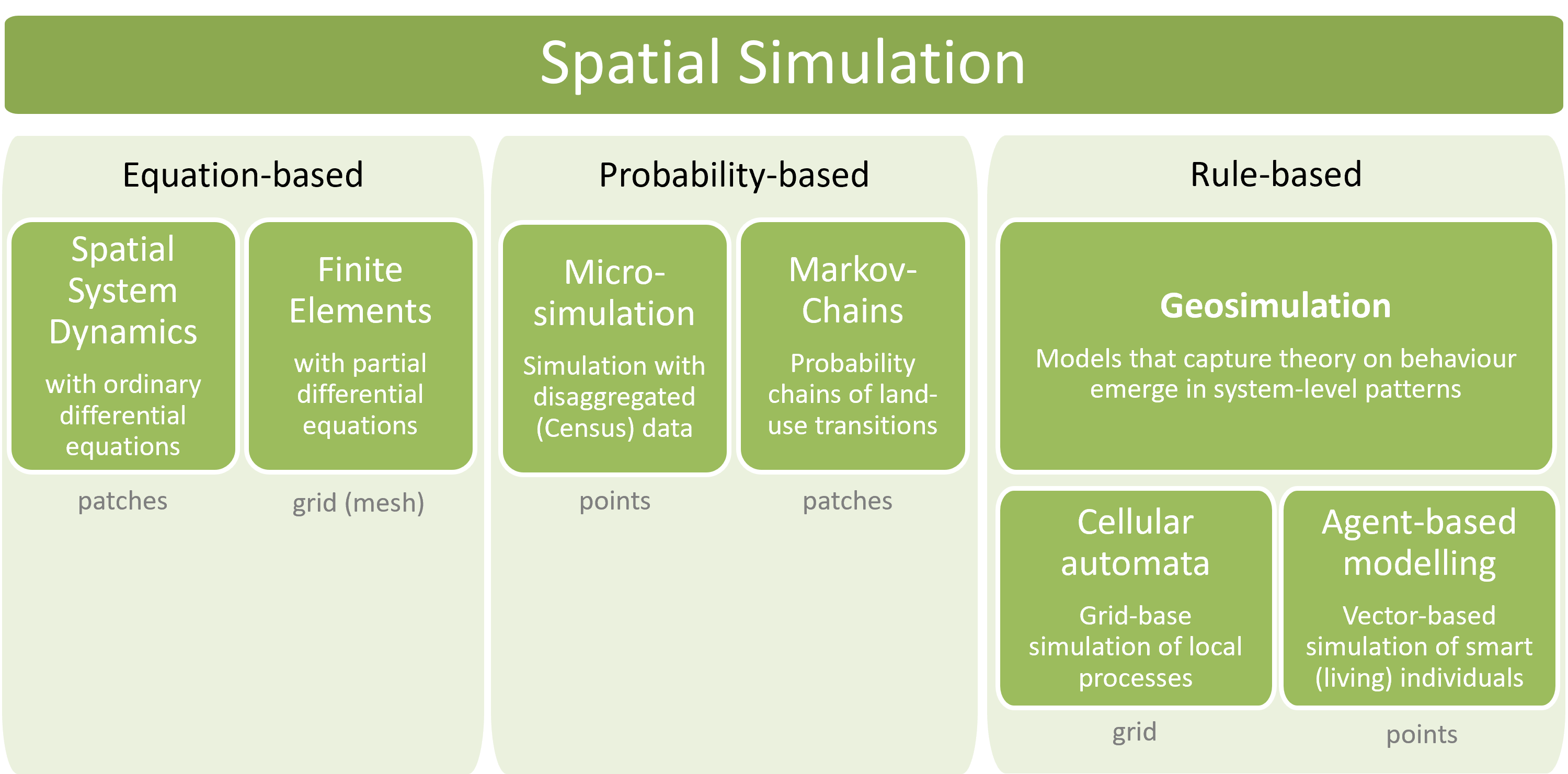
Figure 4.2: Overview of spatially explicit simulation methods.
4.2 Spatial System Dynamics
A straight-forward and simple way to ‘spatialise’ a traditional System Dynamics Model is to assign a specific stock to a specific spatial entity, e.g. to a patch in a vector model or to a cell in a raster model. The forest in a patch is still modelled as an aggregate stock of e.g. biomass. This limits the level of potential spatial disaggregation: patch sizes need to hold forests that are large enough to average out individual randomness of single trees. Stocks are individual instances in the same model with the same parameterisation. Interrelations in the form of in- and out-flows and feedback loops operate independently on each stock. There are no flows between the stocks of neighbouring patches. In short, it is a model of local processes (Neuwirth, Peck, and Simonović 2015).
In Figure 4.3, the system dynamics model governs the forest growth process of several stocks. The input of a model draws from current states of stocks in the respective patches. The actual state of the forest stock at a certain point in time therefore differs from patch to patch. System dynamics software packages can handle simple evolution models without problems.
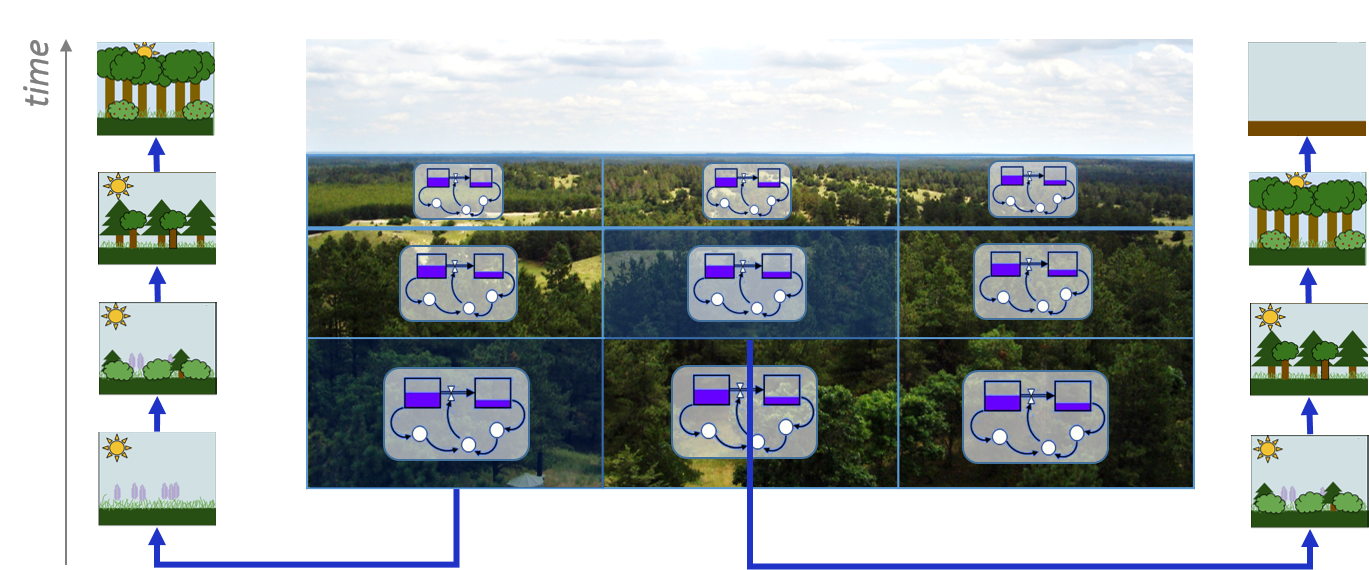
Figure 4.3: A simple spatial Systems Dynamics model of a forest with local stocks of biomass.
Further levels of spatial complexity in a Spatial System Dynamics model consider:
Local parameters Each stock has its individual parameterisation of flows and feedback loops that reflect local conditions. These are still models of local processes, but these processes depend on the local environment, e.g. nutrients, solar radiation, precipitation, etc. In system dynamics software, such local dynamics can be implemented by stock-specific parameterisation of model clones.
Interaction between neighbouring patches To account for the underlying spatial structure of the system flows and feedback loops between stocks of spatially related patches are added. For example, water only flows to downhill patches and seed dispersal only happens between adjacent patches. The system dynamics software thereby needs to be aware of topological relationships between patches. The representation of such spatial relationships is not foreseen in standard System Dynamic software packages.
Multiple stocks per patch that are spatially interrelated An additional degree of complexity is added, if we not only consider one stock per patch, but multiple interrelated stocks per patch, e.g. tree biomass, water, and CO2, number of cattle. In this case we can consider one patch as an individual submodel that is connected with other submodels through their spatial arrangement. We can have different submodels of fundamentally different types, such as forests, agricultural fields and settlements. From a computational perspective, stocks are not anymore individual instances of the same model, but we now have to deal with a multi-model system, where the relation between submodels is governed by their spatial arrangement. Such systems cannot be represented by System Dynamics software alone. Its implementation usually relies on coupling with a GISystem.
Adaptive change of model structure To represent structural changes in complex systems, a model needs to have the capability of self-organisation. In such models, new features emerge, evolve and disappear: a forest may shrink in size or entirely change into a settlement area; an abandoned pasture may turn into a forest; and a road network emerges from the mobility affordances between settlements. Such emergence and self-organisation are fundamental properties of systems. However, capabilities of Spatial System Dynamics models in this regard are rare and related research in its infancy (Neuwirth, Peck, and Simonović 2015). The limitation of system dynamics models to become truly spatial models lies in the modelling approach itself: System Dynamics models represent the world in a top-down manner: system flows are modelled at system level. Although the system can be disaggregated to a certain degree, the smallest entity still needs to represent an aggregated, homogeneous entity that reacts to flows and feedback loops.
4.3 Partial Differential Equation models
In order to model physical processes that are continuous in space and time, it is not enough to model a variable over time, but we need to explicitly include also space as a variable. Typical application examples that interface with geoinformatics would be fluid dynamics, like water turbulence in a river (Figure 4.5), or wind speeds around obstacles (Figure 4.4). Solid models are less relevant for geoinformatics applications. They are mainly used to simulate the behaviour of materials, e.g. deformations of cars in crash simulations.
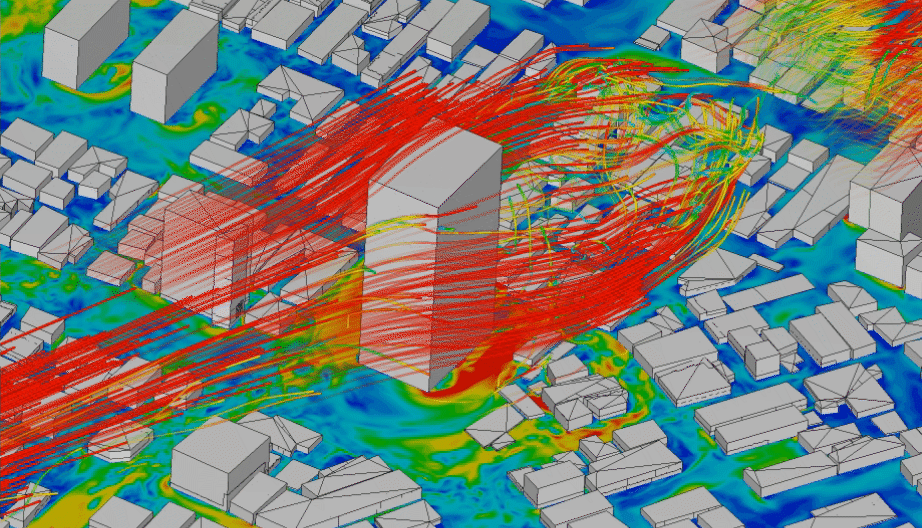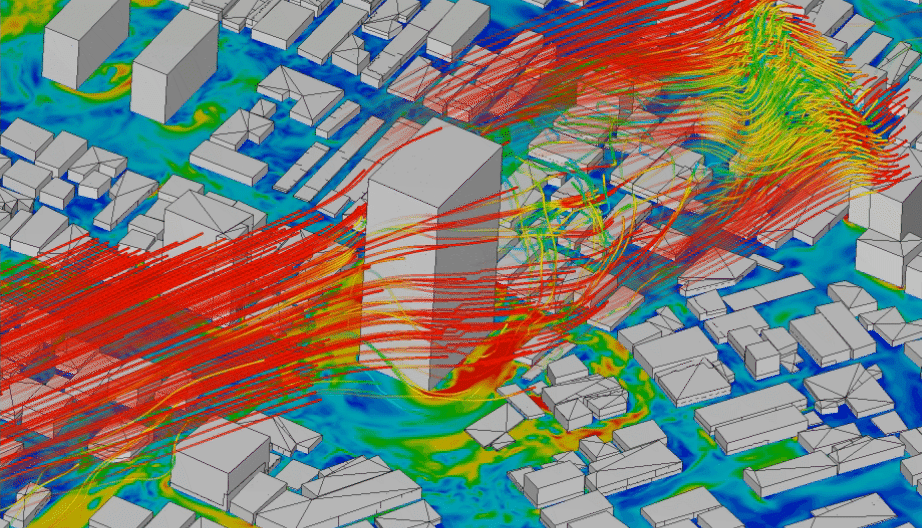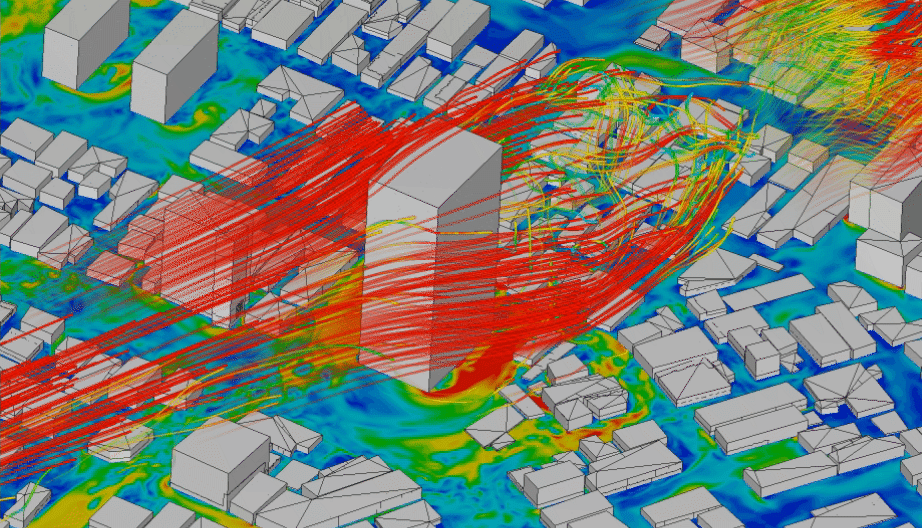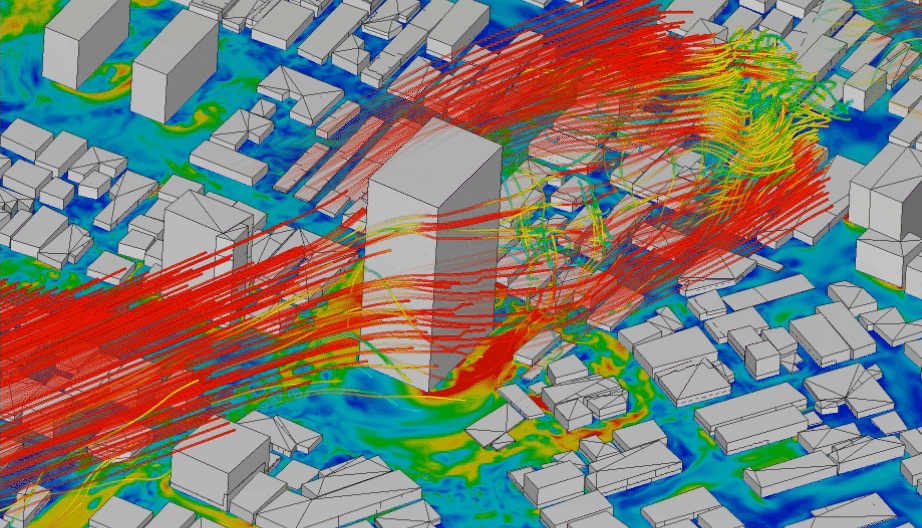
Figure 4.4: CFD simulation of wind around buildings carried out using LBM analysis with SimScale. Animation from: www.simscale.com
Mathematically, we have to move from ordinary differential equations that model a process over time (the system dynamics approach) to partial differential equations (PDE) that model a process in time and space. To solve partial differential equations, we do not just have to dissect time into small time steps, but also dissect space into a mesh (Figure 4.5) - and then again use numerical simulation to approximate the solution in stepwise difference equations from time step to time step and from mesh patch to mesh patch.
As you will guess, the resolution and the structure of the mesh is of great importance for the quality of the model. Areas of steep gradients afford a fine mesh, whereas more homogeneous areas can be wide-meshed to reduce computational costs.
Figure 4.5: Video 0:40 min. Simulation of a cylinder in a wind tunnel on a moving Voronoi mesh, which is refined dynamically. The colour indicates the surface density. The resolution in the right panel is 500x500 Voronoi cells.
According to the type of mesh geometry, we can distinguish Finite Difference methods based on rectangular grids, Finite Element methods based on TINs and Finite Volume methods which usually are based on voxels or Voronoi regions. The spatio-temporal patterns that result from numerical models include stationary and dynamic patchy patterns, oscillations, propagation fronts or spiral waves.
4.4 Probability-based models
Probability-based spatio-temporal models rely on observation data, from which statistical relationships between spatial entities can be inferred. Probabilistic models are purely phenomenological. That means they describe the system without providing any insights into causalities and how a system functions. However, probabilistic models mimic real-world processes often very closely, which makes them perfect candidates for predictive models, like weather forecasts or the prediction of traffic congestions. The only caution that needs to be taken is that these models are only valid within the spatial and temporal frame for which they have been calibrated. Therefore, a probabilistic traffic model for instance cannot predict traffic flows around a new construction site. However, as data nowadays gets more and more abundant, probabilistic models of dynamic system gain momentum. Most prominently, this involves Markov Chain models.
A set of different machine-learning approaches would also fall under the category of correlative, probability-based models. However, the actual mechanism of the process is hidden in these models. The purpose of such “black box” models thus is shifted from understanding systems to predicting systems. A comprehensive discussion of spatio-temporal machine learning approaches would be worth another module.
4.4.1 Markov Chains
Markov Chains are an probabilistic approach for patch-based models. They define the status of a cell in the next time step, based on its own current status and a transition-probability matrix that is derived from (big)data. This matrix is sketched graphically in the diagram in Figure 4.6. For example, in a land-use change model, there might be a 10% probability for a cell with agricultural land use to change its state to urban. The probabilities can either be empirical data gathered from observations of past changes or they can be expert-based. Such ‘memoryless’ transitions, where the next state only depends on the current state are called Markov Chains.
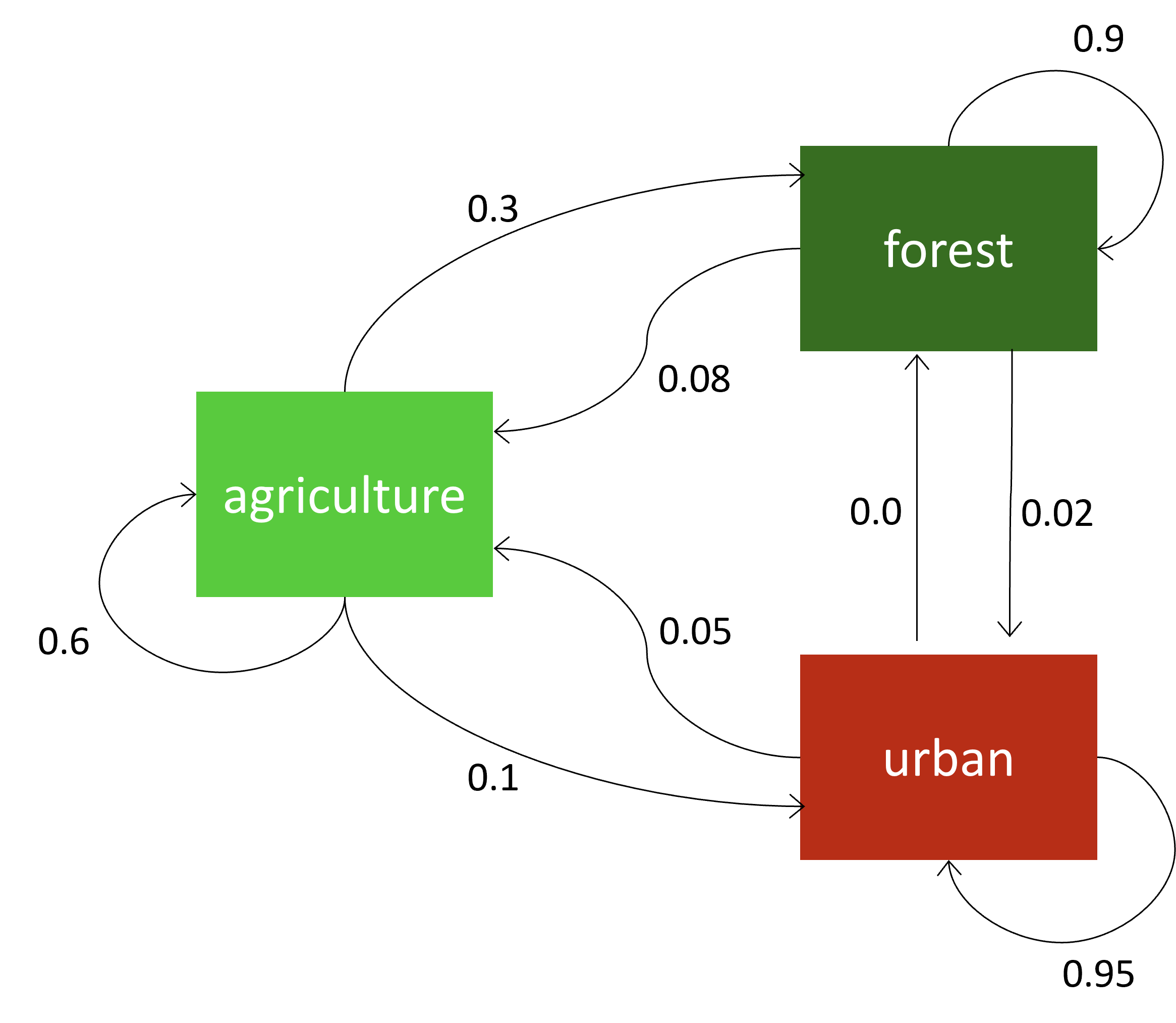
Figure 4.6: A markov chain model for land-use change defines the change probability for the next time step probabilistically from the current state.
The interactive NetLogo model in Figure 4.7 implements the Markov chain transition rules of Figure 4.6. As you run the simulation, you will note that the transition between land use classes is random in space.
Figure 4.7: Netlogo Markov chain model
4.5 Geosimulation
Geosimulation models are bottom-up models, which assume that internal heterogeneity plays an important role for the system’s structure and function. The entities are disaggregated to the level of individuals and very local environments that adapt to each other and interact locally. Thus, Geosimulation is the methodological approach to address questions around complex, living systems. The models that were presented in Lesson 2 to exemplify properties of complex systems are all geosimulation models: flocking, peppered moths, or the virus model.
In the 1970ies Simon Levin introduced the importance of spatial heterogeneity to the ecological community (Levin 1976). Subsequently, modellers demonstrated for many processes that spatial heterogeneity can explain observed behaviour of spatial systems much better than aggregate equation-based models could, e.g. predator-prey stability (Hastings 1977), species diversity (Rosenzweig 1995), or the spread of wildfires in patchy landscapes (M. G. Turner and Romme 1994).
Spatial heterogeneity is at the centre of interest in Geosimulation. Modellers have approached it from two sides: processes in heterogenous landscapes (Cellular Automata models) and heterogeneous individuals that interact locally (Agent-based models). Most often Geosimulation models are hybrid models, where individual agents of an Agent-based model interact with the local environment that is modelled as Cellular Automaton.
With Geosimulation models, we can study, how spatial patterns affect the behaviour of individuals (e.g. route choice), or vice-versa how spatial patterns emerge from the interaction of individuals (e.g. traffic jams).
4.5.1 Agent-based models
In Agent-based models, spatial patterns emerge from heterogeneous individuals that interact locally. Even if agents are located in homogeneous environments, the expected result of such models is a self-organised, spatial pattern. The classic example is the clustering behaviour of social animals, such as flocking birds or schooling fish. The same phenomenon can be observed in groups of pedestrians.
There is no need to define an abstract, system-level parameter like “birth-rate”. Instead, the actual behaviour is implemented in a mechanistic way: individual females meet at the same location and at the same time with a male to mate and to produce offspring. So, Agent-based modellers are programmers that tell the story of the system in a formalised way.
Exercise - geospatial ABM
In this exercise, cows will move on a pasture, where the geometry of the pasture is loaded from a .geojson file. If you successfully implemented the Hello World model of Lesson 1, you are ready to model with geospatial data.
I have commented my code, so that another modeller, who reads the code can easily understand what the code does. This is good practice in programming: I highly recommend that you do the same. Don’t wait with code commenting until you’ve finished, but comment as you go.
And again: make sure that you set your indents correctly. A well-structured code is easier to understand and it is much easier to spot errors!
Prepare the model
- Download the .geojson file of the pasture “Vierkaseralm” near Salzburg. GAMA has a specific folder structure to make referencing geospatial data easier. If you look into your Gama Project, you will find a folder called ‘includes’. Store the pasture file there.
- Create a new model in which 5 cows walk around randomly.
Load the geospatial data into your model
- Load the geospatial data into a global variable of type “file”. Always use relative paths to access files, otherwise your model won’t run on someone else’s computer.
//Load polygon file
file pasture_file <- file("../includes/vierkaser.geojson"); - When you work with geospatial data in GAMA, you always need to explicitely define the bounding box of your model and read it into the predefined global “shape” variable. The command to get the bounding box of a geometry is “envelope()”:
//Define the extent of the study area
geometry shape <- envelope(pasture_file); - Read the geometry of the pasture into a variable:
//read the geometry of the pasture file into a variable
geometry pasture_geom <- geometry(pasture_file); Restrict the cows’ movement
- Set the built-in agent variable “location” to “any_location_in” the pasture, when you create the cows.
//create 5 cow agents that are located within the pasture
create cows number: 5 {
location <- any_location_in (pasture_geom);
} - In the agent section, adjust the movement. The default units, when you work with geospatial data in GAMA are metres and seconds. A speed of 1 would thus be 1 m/s = 3.6 km/h. Let’s slow down the cows and set the speed to 0.5 m/s. You can also set a maximum turning amplitude. Let’s set it to 90 degrees. Finally, you want your cows to stay in the pasture. This can be done with the “bounds” facet.
//behaviour: movement
reflex moveAround {
do wander amplitude: 90.0 speed: 10 #m/#s bounds:pasture_geom;
}Visualise the cows and the pasture
- In the agent section, you need to think about the size of the cow. Remember, that the default unit is a metre. So a circle(1) would be a cow symbol of 1m radius. It will be hard to spot on a pasture that has an extent of 2 x 2km. Try to find a good size!
- In the experiment section, draw the geometry of the pasture. The layers are drawn in the order that you write them. So, first draw the pasture, then the cows. Otherwise the cows would be hidden.
//draw the geometry of the pasture
graphics "pasture_layer"{
draw pasture_geom color: #green;
}Done - we have a basic model. Before we use this model to play around a little bit with it, I share the full code. So that you can compare and continue with the exercise, if anything doesn’t work for you.
See the full code to double-check.
/***
* Name: ExL4a_geospatialABM
* Author: WALLENTIN, Gudrun
* Description: Exercise of the UNIGIS Salzburg optional module
* working with geospatial data
***/
model ExL4a_geospatialABM
global {
//Load polygon file
file pasture_file <- file("../includes/vierkaser.geojson");
//Define the extent of the study area
geometry shape <- envelope(pasture_file);
//read the geometry of the pasture file into a variable
geometry pasture_geom <- geometry(pasture_file);
//Create the agents
init {
//create 5 cow agents that are located within the pasture
create cows number: 5 {
location <- any_location_in (pasture_geom);
}
}
}
// cow agents
species cows skills: [moving] {
//behaviour: movement
reflex moveAround {
do wander amplitude: 90.0 speed: 10 #m/#s bounds:pasture_geom;
}
//visualisation
aspect base {
draw circle (5) color: #black;
}
}
//Simulation
experiment virtual_pasture type:gui {
output {
display map type: opengl{
//draw the geometry of the pasture
graphics "pasture_layer"{
draw pasture_geom color: #green;
}
species cows aspect:base;
}
}
}4.5.2 Cellular Automata
In Cellular Automata, physical, social or ecological processes emerge from heterogeneous landscapes. The size, the shape and the connectivity of a landscape greatly impacts geospatial processes such as floodings, range shifts, dispersal, and colonisation processes, diffusion of air pollution, spread of wild-fires, or land-use change. In Lesson 1, you got acquainted with constructing and visualising a Cellular Automaton with GAMA. In the following exercise we move on to build a geospatial CA.
Exercise - geospatial CA
This exercises complements the geospatial ABM of this lesson. It adds a grazeland-environment to the cow agents.
A Cellular Automaton can be created directly from raster data that is read into a global variable of type “file”. Possible formats are ASCII and GeoTiff. However, in this exercise we construct a grid from vector geometries.
Within the “Vierkaser” pasture property, there are only some regions with open grassland, whereas the rest of the pasture has been overgrown with shrubs and trees.
- The “study_area.geojson” is the bounding box of the Vierkaser property Download,
- the “vierkaser.geojson” is the fenced Vierkaser property Download,
- the “lower_pasture.geojson” is an area with well growing grass within the fenced area Download, and
- the “Hirschanger” pasture is of lower quality within the fenced area Download.
Download each of the files and copy them into your /includes folder. With the following code you can load the data into your model.
//Load geospatial data
file study_area_file <- file("../includes/study_area.geojson");
//fenced area includes shrubs and grassland
file fenced_area_file <- file("../includes/vierkaser.geojson");
//high-quality pasture area
file lower_pasture_file <- file("../includes/lower_pasture.geojson");
//low-quality pasture area
file hirschanger_file <- file("../includes/hirschanger.geojson");Next, we need to set the shape geometry that defines the extent of the model and read the geometry from the vector files, like we have done it in the previous exercise.
See the code
//Define the extent of the study area as the envelope (=bounding box) of the study area
geometry shape <- envelope (study_area_file);
//extract the geometry from the vector data
geometry fence_geom <- geometry(fenced_area_file);
geometry lower_pasture_geom <- geometry(lower_pasture_file);
geometry hirschanger_geom <- geometry(hirschanger_file);Initialise the CA
When we set up (=initialise) the CA, we construct a grid with a cell size of 5m x 5m. Each of the cells has two attributes: the current biomass and the maximum potential biomass per cell with a default value of 0.
See the code
grid grass cell_width:5 cell_height:5 {
float biomass;
float max_biomass <- 0.0;
}To initialise the model we want to set the maximum biomass for each of the pasture areas: the lower pasture can grow up to 10 units of biomass per cell, the Hirschanger has a maximum of 7. Everywhere else within the fence, there are shrubs and the grass biomass can’t grow beyond 1.
To do so, we need to implement a conditional structure (if / else) and we need to do a spatial overlay operation.
if and else
Conditional structures with “if” and “else” are very important in Geosimulation: they can encode behaviour.
IF a condition is true, do something
if <condition> {
do something
}ELSE (the condition above is false) and IF another condition is true, do something else
else if <condition> {
do something else
}ELSE (if nothing of the above is true), do yet another thing
else {
do yet another thing
}for example:
if biomass > 5 {
write "yummieh";
}Spatial overlay
GAMA offers all relevant functions that we need to evaluate overlay. Have a look at´the GAMA Documentation for spatial operators to find out, which spatial operators are available. You will see, it’s quite a few – next to simple distance operators (e.g. closest_to) you will probably recognise the classical topological relations: touches, covers, crosses, intersects, overlaps. Here lies a lot of the power of GAMA’s spatial functionality.
To evaluate, whether a particular cell in the CA grid overlaps the Hirschanger pasture, we could write:
if self overlaps(hirschanger_geom) {
write "This is Hirschanger";
}Of course, it is not only possible to evaluate overlay, but also to perform an overlay operation. A union operation for example is as simple as that:
//union_geom is the union of polygon_A and polygon_B
geometry union_geom <- polygon_A + polygon_B;Creating a CA from a raster file
You can create a Cellular Automaton directly from a raster file. The input data needs to be either in ESRI’s .asc or the .tif format, and you also should provide the epsg code (here it is Web Mercator, epsg 3857) to make sure the raster projected correctly.
In the grid section, you can then construct the CA directly from the raster file. It will read the raster’s cell values into a built-in grid variable that is called grid_value. As it is built-in, you don’t have to declare grid_value, but can use it right away. The below code, simply writes each of the cell values into the console:
global {
//declare the raster import file
file my_raster_data <- grid_file("../includes/some_raster.tif", 3857);
}
grid myCA file: my_raster_data {
init {
write grid_value;
}
}
Now, try to implement the code that sets the current and maximum biomass:
- Lower pasture: max_biomass = 10, and biomass = 2
- Hirschanger pasture: max_biomass = 7, and biomass = 2
- everywhere else within the fenced area: max_biomass = 1, and biomass = 1
See the code
//assign the value of 1 as the max. biomass within the fenced area
if self overlaps(fence_geom){
//set the maximum biomass of a grazeland cell to 1
max_biomass <- 1.0;
biomass <- 1.0;
}
//if the cell overlaps the lower pasture: assign the value of 10 to the biomass (this overwrites the biomass=1 within the fenced area)
if self overlaps(lower_pasture_geom){
max_biomass <- 10.0;
biomass <- 2.0;
}
//if it is not in lower pasture, but it overlaps Hirschanger: assign the value of 7 to the biomass ("else if" overwrites the fenced area, but not the lower pasture)
else if self overlaps(hirschanger_geom){
max_biomass <- 7.0;
biomass <- 2.0;
}Make the CA dynamic
Finally, we let the CA grow grass in a reflex. Add a reflex that increases the biomass of each cell at each time step. The logistic growth function makes sure that the grass can’t grow beyond its maximum, and the update_colour reflex updates the colour to visualise the biomass change in the simulation.
To avoid a division by zero, we also need to restrict this reflex to cells within the fenced area with a max_biomass > 0. This could be done by using an if-condition within the reflex, but alternatively and more efficiently also the when facet can be used:
// let grass grow until its maximum potential
reflex grow_grass when: max_biomass > 0 {
//logistic growth: N + r*N*(1-N/K)
biomass <- biomass + grass_growth_rate * biomass * (1 - biomass / max_biomass);
color <- rgb([0, biomass * 15, 0]);
}
Done. The Cellular Automaton model reads a geospatial pasture polygon and models grass growth on that pasture.
See the full code for the CA pasture model.
Watch the grazeland get a more intense green colour. If that happens too quickly: refresh the simulation, reduce the simulation speed slider and start again.
/***
* Name: Ex L4b_geospatialCA
* Author: WALLENTIN, Gudrun
* Description: Exercise of the UNIGIS Salzburg optional module
* Constructing a Cellular Automaton of grass growth from geospatial data
***/
model ExL4b_geospatialCA
global {
//Load geospatial data
file study_area_file <- file("../includes/study_area.geojson");
//fenced area includes shrubs and grassland
file fenced_area_file <- file("../includes/vierkaser.geojson");
//high-quality pasture area
file lower_pasture_file <- file("../includes/lower_pasture.geojson");
//low-quality pasture area
file hirschanger_file <- file("../includes/hirschanger.geojson");
//grass regrowh rate
float grass_growth_rate <- 0.1;
//Define the extent of the study area as the envelope (=bounding box) of the study area
geometry shape <- envelope (study_area_file);
//extract the geometry from the vector data
geometry fence_geom <- geometry(fenced_area_file);
geometry lower_pasture_geom <- geometry(lower_pasture_file);
geometry hirschanger_geom <- geometry(hirschanger_file);
init {
ask grass {
color <- rgb([0, biomass * 15, 0]);
}
}
}
//The cellular automaton represents the grazeland
grid grass cell_width:5 cell_height:5 {
float biomass;
float max_biomass <- 0.0;
init {
//assign the value of 1 as the max. biomass within the fenced area
if self overlaps(fence_geom){
//set the maximum biomass of a grazeland cell to 1
max_biomass <- 1.0;
biomass <- 1.0;
}
//if the cell overlaps the lower pasture: assign the value of 10 to the biomass (this overwrites the biomass=1 within the fenced area)
if self overlaps(lower_pasture_geom){
max_biomass <- 10.0;
biomass <- 2.0;
}
//if it is not in lower pasture, but it overlaps Hirschanger: assign the value of 7 to the biomass ("else if" overwrites the fenced area, but not the lower pasture)
else if self overlaps(hirschanger_geom){
max_biomass <- 7.0;
biomass <- 2.0;
}
}
// let grass grow until its maximum potential
reflex grow_grass when: max_biomass > 0 {
//logistic growth: N + r*N*(1-N/K)
biomass <- biomass + grass_growth_rate * biomass * (1 - biomass / max_biomass);
color <- rgb([0, biomass * 15, 0]);
}
}
//Simulation
experiment virtual_pasture type:gui {
output {
display map type: opengl{
//draw the geometry of the pasture with the defined color value
grid grass ;
}
}
}4.5.3 Combined Geosimulation model
We could now combine the Agent-based cow model and the dynamic grass growth of the Cellular Automaton to a spatially explicit cow-pasture model. Actually, such combination of ABM and CA is the rule rather than the exception. It is the combination of smart individuals interacting in and with a dynamic environment (Figure 4.8).
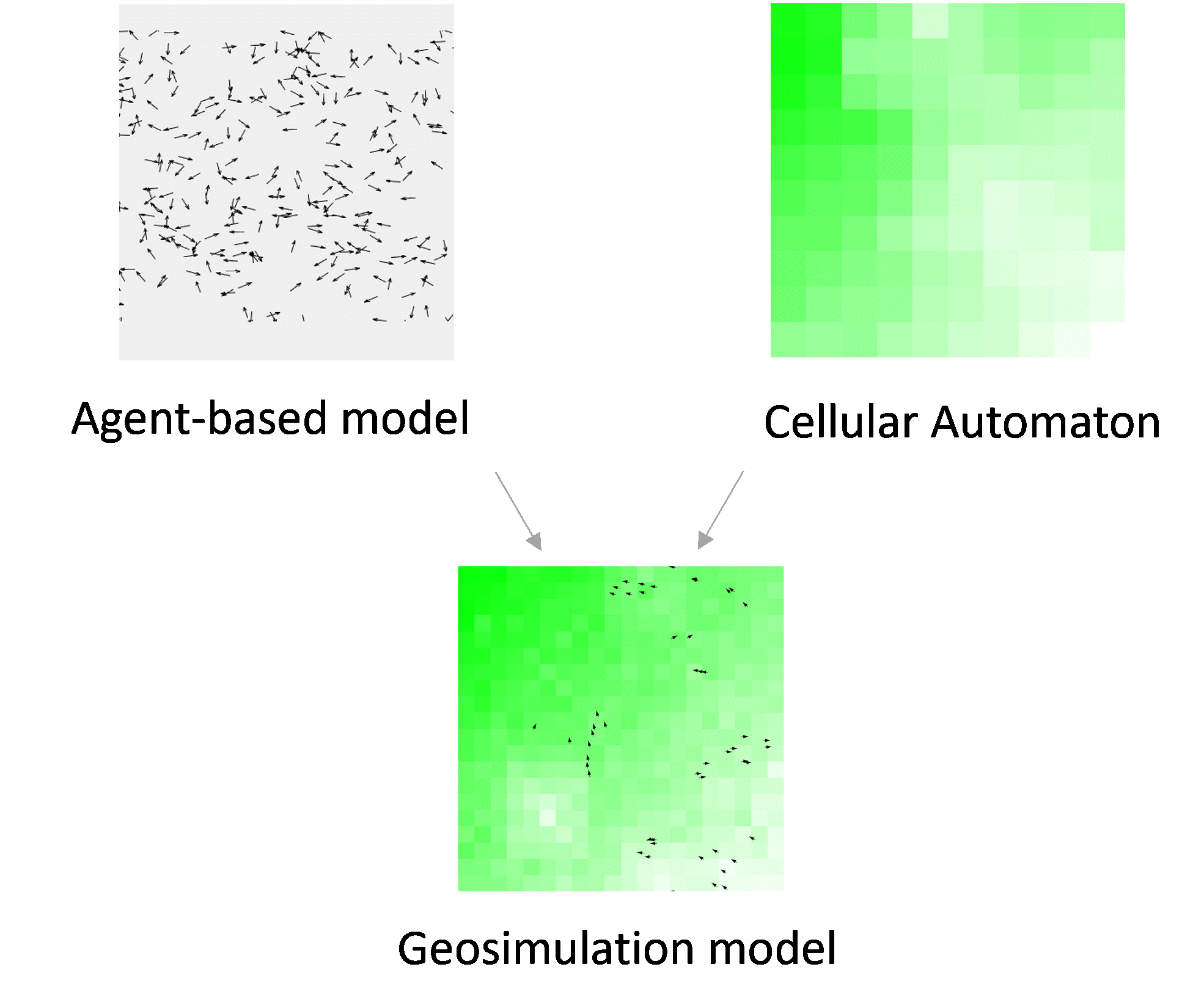
Figure 4.8: A geosimulation model often integrates Agent-based models with Cellular Automata to represent complex living systems.
Another common representation of space is a network, e.g. for traffic simulation or for an abstract representation of topological relationships as for example in communication networks. Recent progress in the coupling of modelling frameworks with GIS enable advanced spatial data handling in agent-based models that to date were restricted to comparatively simple functionalities in terms of spatial analysis.
Exercise - Geosimulation pasture model
The last exercises of this lesson combines the two geospatial models of this lesson. Try to integrate the code yourself, before you look at the solution!
See the full code for the integrated pasture model.
/***
* Name: Ex L4c_geospatialABM
* Author: WALLENTIN, Gudrun
* Description: Assignment solution of the UNIGIS Salzburg optional module
* working with geospatial data
***/
model ExL4c_geospatialABM
global {
//Load geospatial data
file study_area_file <- file("../includes/study_area.geojson");
//fenced area includes shrubs and grassland
file fenced_area_file <- file("../includes/vierkaser.geojson");
//high-quality pasture area
file lower_pasture_file <- file("../includes/lower_pasture.geojson");
//low-quality pasture area
file hirschanger_file <- file("../includes/hirschanger.geojson");
//grass regrowh rate
float grass_growth_rate <- 0.1;
//Define the extent of the study area as the envelope (=bounding box) of the study area
geometry shape <- envelope (study_area_file);
//extract the geometry from the vector data
geometry fence_geom <- geometry(fenced_area_file);
geometry lower_pasture_geom <- geometry(lower_pasture_file);
geometry hirschanger_geom <- geometry(hirschanger_file);
geometry pasture_geom <- lower_pasture_geom + hirschanger_geom;
//Create the agents
init {
//create 5 cow agents that are located within the pasture
create cows number: 5 {
location <- any_location_in (pasture_geom );
}
ask grass {
color <- rgb([0, biomass * 15, 0]);
}
}
}
// cow agents
species cows skills: [moving] {
//behaviour: movement
reflex moveAround {
do wander amplitude: 90.0 speed: 10 #m/#s bounds:pasture_geom;
}
//visualisation
aspect base {
draw circle (5) color: #black;
}
}
//The cellular automaton represents the grazeland
grid grass cell_width:5 cell_height:5 {
float biomass;
float max_biomass <- 0.0;
init {
//assign the value of 1 as the max. biomass within the fenced area
if self overlaps(fence_geom){
//set the maximum biomass of a grazeland cell to 1
max_biomass <- 1.0;
biomass <- 1.0;
}
//if the cell overlaps the lower pasture: assign the value of 10 to the biomass (this overwrites the biomass=1 within the fenced area)
if self overlaps(lower_pasture_geom){
max_biomass <- 10.0;
biomass <- 2.0;
}
//if it is not in lower pasture, but it overlaps Hirschanger: assign the value of 7 to the biomass ("else if" overwrites the fenced area, but not the lower pasture)
else if self overlaps(hirschanger_geom){
max_biomass <- 7.0;
biomass <- 2.0;
}
}
// let grass grow until its maximum potential
reflex grow_grass when: max_biomass > 0 {
//logistic growth: N + r*N*(1-N/K)
biomass <- biomass + grass_growth_rate * biomass * (1 - biomass / max_biomass);
color <- rgb([0, biomass * 15, 0]);
}
}
//Simulation
experiment virtual_pasture type:gui {
output {
display map type: opengl{
//draw the geometry of the pasture
grid grass;
species cows aspect:base;
}
}
}